A new discovery has been made in the world of mathematics, as a team of researchers from various institutions has found a way to make tiles that can fill an infinite plane without any repetition or gaps. The tiles take the shape of a hat and were discovered by David Smith, a retired engineer, after he had been working on a similar puzzle for years. The team of researchers created two different proofs to verify the tiling and to show that it is aperiodic. This means that it can never repeat itself in any direction. The discovery of this new type of tiling opens up new avenues for mathematicians to explore and study.
A Shape Hobbyist Discovers the Einstein Tiling Problem
David Smith, a retired printing technician and self-proclaimed shape hobbyist from Bridlington, East Yorkshire, England, may have finally solved the elusive Einstein problem. This problem pertains to finding a single shape that can tile a plane, or an infinite two-dimensional flat surface, in a non-repeating pattern, which is known as an aperiodic monotile or an Einstein.
The term “Einstein” originated from the German phrase “ein stein,” meaning “one stone” or “one tile,” that describes a shape that can tile a plane without translational symmetry. Typical wallpaper or tiled floors have an infinite pattern that repeats periodically, and mathematicians have long sought to find a shape that tiles a plane without such symmetry.
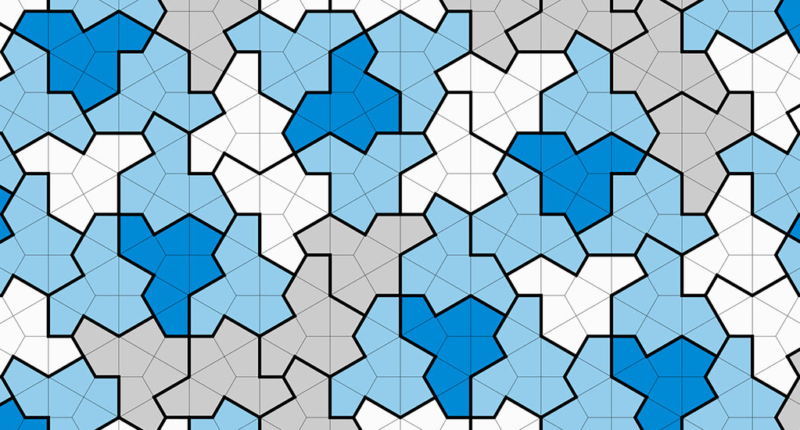
Mr. Smith, who enjoyed math in high school but did not excel at it, has been fascinated by the Einstein problem for years. He has been experimenting and playing with shapes as a hobby and last November, after a decade of failed attempts, he suspected that he may have finally solved the problem. He called his proposed Einstein “the hat” because of its resemblance to a fedora, and it has now been proven true by Mr. Smith and three co-authors with mathematical and computational expertise in a new paper.
According to the researchers, the “hat” is an aperiodic monotile that has no clear structural similarity with any of the familiar classes of structures, making it a remarkable discovery. The paper has not yet been peer-reviewed, but Joshua Socolar, a physicist at Duke University who read an early copy of the paper provided by The New York Times, said that the mathematical result raises some interesting physics questions. He added that encountering or fabricating a material with this type of internal structure could be a possibility.
Mr. Smith’s proposed Einstein has gained attention from the scientific community due to its unique tiling pattern. Joan Taylor, an independent researcher in Burnie, Tasmania, and Dr. Socolar previously discovered a hexagonal monotile made of disconnected pieces, which some consider to have stretched the rules. They also found a connected 3-D version of the Socolar-Taylor tile.
In conclusion, Mr. Smith’s discovery of an Einstein tiling is a significant milestone in the mathematics of tiling, and it could potentially lead to further studies in physics and materials science.
A Retired Printing Technician Solves the Einstein Tiling Problem
The Einstein tiling problem pertains to the search for a single shape that can tile a plane without translational symmetry, or an aperiodic monotile. In 1961, Hao Wang conjectured that such a set of shapes was impossible, but his student Robert Berger proved the conjecture wrong by discovering an aperiodic set of tiles. Since then, the challenge has been to find the minimum number of tiles that can accomplish this.
Sir Roger Penrose, a mathematical physicist at the University of Oxford, reduced the number of tiles to two in the 1970s, and others have since discovered pairs of their own. The ultimate goal was to find a single tile that could tile a plane in a nonrepeating pattern, which David Smith, a retired printing technician and shape hobbyist from Bridlington, East Yorkshire, England, may have achieved.
Mr. Smith suspected that he had found an Einstein tiling, or an aperiodic monotile, after a decade of experimentation with shapes. His proposed Einstein, which he called “the hat,” resembles a fedora and has been proven true in a new paper by Mr. Smith and three co-authors with mathematical and computational expertise. The hat is a strikingly simple shape that makes only nonperiodic patterns, making it a significant milestone in the mathematics of tiling.
Joseph Myers, a co-author and software developer in Cambridge, England, executed two proofs for the hat’s aperiodic monotiling using a traditional method and a new technique. The proofs were described as complicated by Sir Roger Penrose, but he was extremely intrigued by the hat’s simplicity and considered it a tour de force.
In conclusion, Mr. Smith’s discovery of the hat tiling has garnered attention from the scientific community, as it represents a significant breakthrough in the pursuit of the Einstein tiling problem.
David Smith’s Discovery of an Einstein Tiling
David Smith, a retired printing technician and shape hobbyist from Bridlington, East Yorkshire, England, has discovered an “einstein,” or an aperiodic monotile. His discovery came after a decade of experimenting with shapes and using the PolyForm Puzzle Solver, software developed by Jaap Scherphuis, a tiling enthusiast and puzzle theorist in Delft, the Netherlands. When he found a tile that seemed to fill the plane without a repeating pattern in November 2022, he emailed Craig Kaplan, a co-author and computer scientist at the University of Waterloo.
Dr. Kaplan built on previous research and generated larger and larger swaths of hat tiles using his algorithm. With this raw data, Mr. Smith and Dr. Kaplan studied the tiling’s hierarchical structure by eye. Dr. Kaplan unlocked telltale behavior that opened up a traditional aperiodicity proof. The method involves defining a set of four “metatiles” that assemble into four larger shapes that behave similarly, which was enough to show that the hat tiling can never tile periodically.
The Einstein Tiling Problem
The Einstein tiling problem pertains to the search for a single shape that can tile a plane without translational symmetry, or an aperiodic monotile. In 1961, Hao Wang conjectured that such a set of shapes was impossible, but his student Robert Berger proved the conjecture wrong by discovering an aperiodic set of tiles. Since then, the challenge has been to find the minimum number of tiles that can accomplish this.
Mr. Smith’s Experimental Process
Mr. Smith’s process involved producing a first batch of 32 copies of a potential tile using a Silhouette cutting machine from card stock. He would fit the tiles together, with no gaps or overlaps, like a jigsaw puzzle, reflecting and rotating tiles as necessary. He found this process to be meditative and provided a better understanding of how a shape tessellates.
The Hat Tiling
Mr. Smith’s proposed Einstein, which he called “the hat,” resembles a fedora and has been proven true in a new paper by Mr. Smith and three co-authors with mathematical and computational expertise. The hat is a strikingly simple shape that makes only nonperiodic patterns, making it a significant milestone in the mathematics of tiling. However, at the risk of seeming picky, some may wonder whether the hat tiling is a two-tile, not one-tile, set of aperiodic monotiles because it uses reflections – the hat-shaped tile and its mirror image.
Conclusion
Mr. Smith’s discovery of the hat tiling represents a significant breakthrough in the pursuit of the Einstein tiling problem. It was clear that something unusual was happening with the shape, and Dr. Kaplan’s algorithm generated larger and larger swaths of hat tiles. Dr. Kaplan and Mr. Smith’s study of the tiling’s hierarchical structure by eye led to the discovery of telltale behavior that opened up a traditional aperiodicity proof.
A single tile that tessellates in a non-periodic manner has been found after over half a century of searching. Previously, it was only thought possible to tessellate the plane with multiple shapes in a non-periodic manner, but the “einstein” tile discovered by David Griffeath, a mathematician at the University of Wisconsin, disproved this. A subsequent development saw a pair of shapes discovered that could tessellate in a non-periodic manner, but the hunt for a single tile that could do this was ongoing.
The “holy grail” of mathematical tiling pursuits was whether it was possible to tessellate the plane with one tile in a non-periodic manner. Now, a mathematician named David Smith has discovered such a tile, which he calls “the hat,” so named due to its distinctive shape. The hat is a polykite – made up of eight kites – and can be tessellated to form a pattern that does not repeat. In fact, Dr. Craig S. Kaplan of the University of Waterloo, who helped to prove that the hat was an aperiodic tile, noted that the hat was not a new geometric invention, but that it had been “hiding in plain sight.”
The hat is made by “fiddling about” with Jaap Scherphuis’ PolyForm Puzzle Solver software before using a Silhouette cutting machine to produce a batch of card stock copies that are fitted together like a jigsaw puzzle. The resulting pattern is non-periodic, meaning that it never repeats, but a question remains whether the hat can be considered a one-tile set or a two-tile set since it includes reflections. However, even using its reflection, the hat counts as a monotile.
Moreover, a second tile that can tessellate in a non-periodic manner was discovered by Mr. Smith. The turtle, a polykite made of ten kites, was initially overwhelming for Dr. Kaplan as he was already busy with the hat, but a third mathematician, Joseph Myers, connected the hat and the turtle, ultimately discovering an entire family of shapes, a continuous, uncountable infinity of einsteins that morph one to the next.
The hat has been found to be an aperiodic tile, meaning that it cannot be tiled periodically, despite being laid out on a hexagonal grid, which is as periodic as one can get. The discovery of the hat and the turtle offer exciting new opportunities for the field of mathematical tiling, providing new tools for proving aperiodicity.
Dr. Goodman-Strauss considers the new technique as an essential part of the discovery, and it might only be understood by a few connoisseurs. He admitted that it took him a couple of days to digest the information and was later “thunderstruck” by the results. Meanwhile, Mr. Smith admitted he was no help in the research paper but was amazed to see it come together. He praised the illustrations, stating that he was more of a “pictures person.” A video featuring the discovery was also released, created by Craig Kaplan.
Don’t miss interesting posts on Famousbio